Dijksrta(SPF) 算法

1. 简介

  Dijksrta 算法，一种用来计算途中最短路径的贪心算法，通常用来计算单源最短路径；又称为 SPF 算法，即 Shortest Path First，最短路径优先算法；

  最开始，只是用来找两个顶点之间的最短路径；后面最常见的变体是：固定一个顶点作为源节点，找到途中所有其他的节点的最短路径，产生一个最短路径树；

2. 思想

  从相邻节点开始，选择最近的节点，当做下一个点，计算这个从起始点经过该点到达其他所有节点的距离，更新最短距离数据，已经选取过的点就是确定了最短路径的点，不再参与下一次计算，重复上述过程，直至所有节点被访问；典型贪心算法思想；

3. 步奏

1. 初始化
   • 将源节点的距离设置为 0，其他所有节点的距离设置为 无穷大；
   • 源节点标记为“已访问”；开始找与源节点相连的节点；
2. 选择当前值最短路径的节点：
   • 在所有没有访问的节点之中，寻找一个距离源节点最近的节点；
3. 更新邻居节点距离；
   • 对当前的每一个令居节点，计算通过当前节点到达该邻居节点的距离；如果小于当前已知的距离，则更新邻居节点的距离；
4. 重复知道所有的节点都已访问：
   • 将当前节点标记为 “已访问”，然后选择下一个未访问的且距离源节点最近的节点，重复上述过程；
5. 输出最短路径：
   • 一旦所有节点都被访问，算法结束；此时，输出源节点到各个节点的最短路径；

4. 示例

当前有一个图：

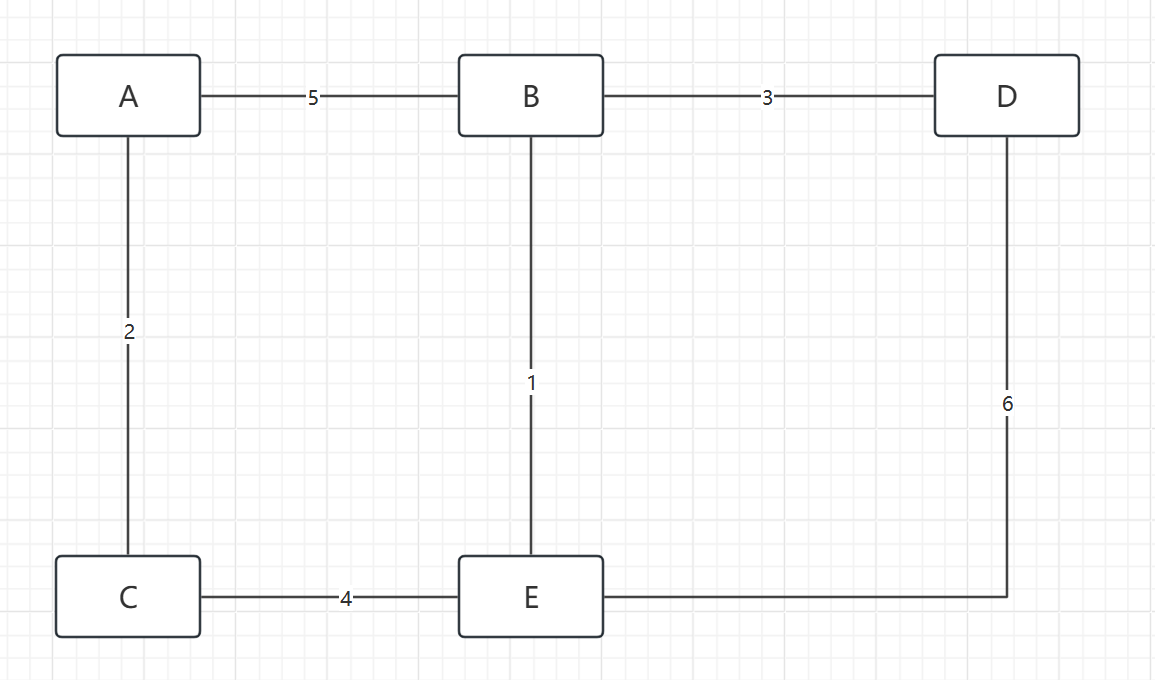
计算由 A 到所有节点的最短路径！

1. 初始化距离数组：distance{A:0,B:-1,C:-1,D:-1,E:-1}；已访问节点：无；
2. A 相邻节点，开始进行访问（也可以认为，选择当前未访问节点，距离起点最近的，当然是 0 的A点）；distance{A:0,B:5,C:2,D:-1,E:-1}；已访问节点：A；
3. 选择当前最短的路径节点，即选择 C 点开始进行访问 C 的邻居；distance{A:0, B:5, C:2, D:-1, E:6}；已经访问的节点：A,C；
4. 选择当前最短的路径节点，即选择 B，更新：distance = {A:0, B:5, C:2, D:8, E:6}；已访问节点：A,C,B；
5. 选择当前最短路径节点，即选择 E，更新：distance = {A: 0, B: 5, C: 2, D: 8, E: 6}；已访问：A,C,B,E；
6. 选择当前最短路径节点，即 D；因为 D 没有未访问的邻居，且已经所有节点都访问了；算法结束；
7. 结果：从 A 点出发：distance = {A: 0, B: 5, C: 2, D: 8, E: 6}；

5. 复杂度

1. 时间复杂度分析：对于没有任何优化的迪杰斯特拉算法来说，实际上等价于每次遍历了整个图的所有节点来寻找顶点集中符合条件的元素；然后遍历所有的边一次；即算法时间复杂度为：O(|V|² + |E|);
2. 可以采用二叉堆、斐波那契堆用作优先队列来进行优化；

6. 应用

1. 网络路由：OSPF 协议，IS-IS 协议；
2. 地图和导航系统；
3. 图像处理；
4. 社交网络分析；
5. ......

7. 总结

  迪杰斯特拉算法是经典的图论算法；是单源最短路径问题的重要算法；